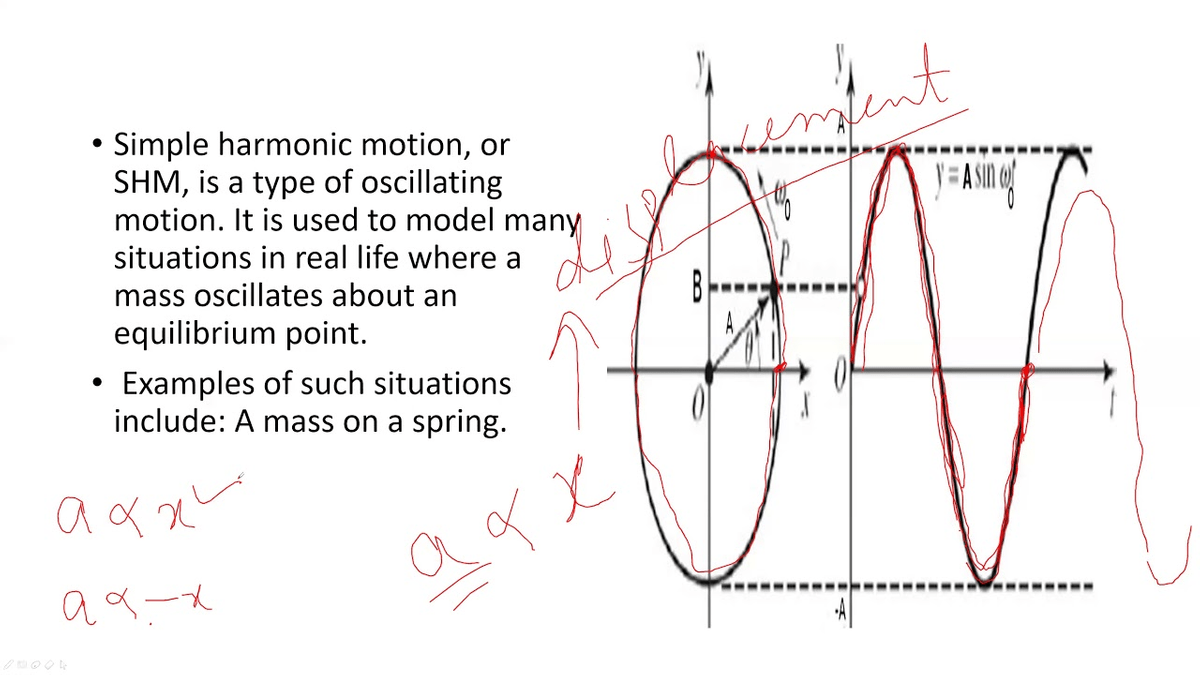
At the maximum displacement x, the spring is under its greatest tension, which forces the mass upward. Simple harmonic motion shown both in real space and phase space. The motion of the block on a spring in SHM is defined by the position x(t) = Acos\(\omega\)t + \(\phi\)) with a velocity of v(t) = −A\(\omega\)sin(\(\omega\)t + \(\phi\)). A specific example of a simple harmonic oscillator is the vibration of a mass attached to a vertical spring, the other end of which is fixed in a ceiling. The acceleration of an object oscillating in simple harmonic motion is: a 2 x. The motion of a particle moving along a straight line with an acceleration whose direction is always towards a fixed point on the line and whose magnitude is proportional to the distance from the fixed point is called simple harmonic motion.